Correcciones en las Transmisiones por Engranajes Cilíndricos de Dientes
Rectos (página 2)

Partes: 1, 2

3. Corrección de
altura o correccción compensada de las ruedas
dentadas.

En ocasiones existen limitaciones en cuanto a la
distancia entre centros a utilizar, es decir la misma no puede
ser elegida libremente. Por ejemplo puede darse el caso de que en
una pareja de engranajes ya diseñada y construida durante
la explotación, los dientes del piñón
resulten más débiles que los de la corona. Ante
esta situación el diseñador puede decidir para
mejorar el comportamiento
de la transmisión dar una correccción positiva al
piñón y una negativa de la misma medida a la corona
; de tal manera que el engranaje en su conjunto quede compensado.
En este caso se mantiene la distancia entre centros, pudiendo
utilizarse la misma carcaza. Cuando se corrige una pareja de
engranajes y la misma corrección positiva Xp que se le da
al piñón, se le da negativa a la corona Xc; estamos
en presencia de una corrección de altura o
corrección compensada de las ruedas dentadas. Es
decir:

Xp = – Xc.

Xå
= Xp + Xc = 0.

A la suma de los coeficientes de corrección del
piñón y de la corona se le llama coeficiente
sumario de corrección ( Xå ) .

Debe tenerse en cuenta a la hora de dar una
corrección de altura que para hacer la rueda corregida
positivamente se necesita un semiproducto mayor, y que para la
corregida negativamente un semiproducto menor.

En la tabla # 2 se muestran las expresiones para el
cálculo de los parámetros geométricos de una
transmisión por engranajes con corrección de
altura.

Tabla # 2: Parámetros geométricos de las
ruedas dentadas con corrección de altura.

Parámetro	Símbolo	Expresión de cálculo
paso	t	p .m
diámetro de paso	dp	m.z
diámetro básico	db	dp.cosa c
diámetro primitivo	dw	db/cosa w
diámetro exterior	da	m.(z + 2.ha + 2.X)
diámetro interior	df	m.(z – 2. (ha+c) +2.X)
distancia entre centros	aw	m. Zå /2
Grueso del diente:
por la circ. básica	Sb	db.( Sp/dp + inva c)
por la circ. de paso	Sp	p .m / 2 + 2.m.X. tana c
por la circ. exterior	Sa	da.(Sp/dp+inva c-inva e)

Las expresiones de la tabla anterior sirven tanto para
el piñón como a la corona, siempre y cuando se
coloquen los valores de
número de dientes (Z) y coeficiente de corrección
(X) con su respectivo signo para la rueda que se esté
calculando.

En las correcciones de altura producto de
que el aumento de diámetro de una rueda es proporcional a
la disminución en diámetro de la otra, la distancia
entre centros es igual que para un engranaje normal con los
mismos números de dientes. El ángulo de
montaje a
w también se mantiene igual al
ángulo de la cremallera a c .

Corrección angular de los engranajes.

En ocasiones para atenuar determinada falla del dentado,
o para llevar una pareja de engranajes a una distancia entre
centros mayor o menor de la que tendrían si fueran
normales se utilizan las correcciones angulares. Estamos en
presencia de una corrección angular cuando el coeficiente
de corrección sumario es diferente de cero, es decir el
valor de
corrección positiva que se le da a una rueda no coincide
con el valor de corrección negativa que se le da a la
otra. Se pueden presentar varios casos a saber:

a) X1 = + X2= – pero de valor diferente.

b) X1 = – X2= + pero de valor diferente.

c) X1 = – X2= –

d) X1 = + X2= +

e) X1 = + X2= 0

f) X1 = – X2= 0

g) X1 = 0 X2= +

h) X1 = 0 X2= –

De todos los casos anteriores el más
lógico y usual en la práctica es el caso d). Cuando
se esta en presencia de dicho caso, producto de
que de la circunferencia de paso hacia arriba los dientes se
hacen más estrechos, y de que la circunferencia primitiva
va a estar por encima de la circunferencia de paso, los
engranajes tienden a "encajarse", es decir a no conservar la
holgura radial relativa. Debido a esto los dientes se recortan en
su punta. En realidad para evitar tener que recortar los dientes
después de maquinados lo que se hace es hacerlos
ligeramente más cortos en una magnitud (
D y ) denominada
coeficiente de desplazamiento invertido. Esto se logra eligiendo
el diámetro exterior del semiproducto ligeramente inferior
al calculado por la corrección. Si el coeficiente de
corrección sumario Xå es positivo se dice que la
corrección es angular positiva, y viceversa. En la tabla #
3 se dan todas las expresiones para el cálculo de una
transmisión por engranajes con corrección
angular.

Tabla # 3: Parámetros geométricos de las
ruedas dentadas con corrección angular.

Parámetro	Símbolo	Expresión de cálculo
paso	t	p .m
diámetro de paso	dp	m.z
diámetro básico	db	dp.cosa c
diámetro primitivo	dw	db/cosa w
diámetro exterior	da	m.(z + 2.ha + 2.X – 2.D .y )
diámetro interior	df	m.(z – 2. (ha+c) + 2.X )
coef. de desp. invertido	D y	Xå + 0,5 Zå – awx / m
distancia entre centros	awx
ángulo de montaje	a w
Grueso del diente:
por la circ. básica	Sb	db.( Sp/dp + inva c)
por la circ. de paso	Sp	p .m / 2 + 2.m.X.tan.a c
por la circ. exterior	Sa	da.(Sp/dp+inva c-inva e)

4. Aspectos
geométricos a tener en cuenta a la hora de dar una
corrección.

Para elegir adecuadamente el valor del coeficiente de
corrección X para la rueda que se esté
diseñando hay que tener en cuenta varios criterios en
dependencia de si se va a dar una corrección positiva o
negativa a la rueda, y además realizar también
algunos chequeos al conjunto de las dos ruedas en dependencia si
se trata de una corrección angular positiva o negativa, o
una corrección de altura.

Aspectos a chequear en las ruedas que se corrigen
negativamente.

El máximo valor del coeficiente de
corrección negativo que se puede dar a una rueda se
determina por la expresión:

En este caso Z es el número de dientes de la
rueda que se corrige negativamente.

Aspectos a chequear en las ruedas que se corrigen
positivamente.

El espesor del diente por la circunferencia exterior
debe ser mayor o igual a a 1/4 del valor del módulo para
evitar que los dientes se partan por la punta.

Aspectos a chequear en las correcciones angulares
positivas o en correcciones de altura corrigiendo positivamente
el piñón y negativamente la
corona.

En estos casos el coeficiente de recubrimiento tiende a
disminuir, por lo que hay que garantizar que no se pierda el
contacto ininterrumpido de los dientes.

Las correcciones angulares negativas o de altura
corrigiendo negativamente el piñón y positivamente
la corona tienen muy poca aplicación práctica; no
obstante en estos casos no hay que chequear el coeficiente de
recubrimiento, pués el mismo aumenta.

Fallas en las transmisiones por engranajes.

Las transmisiones por engranajes pueden sufrir
múltiples deterioros durante su funcionamiento, no
obstante las fallas más comunes son:

a) Picadura o careado. Esta falla se caracteriza por el
desprendimiento de partículas de la superficie del diente
producto de la acción del lubricante. Estos
desprendimientos aparecen en la zona cercana al polo por encima y
por debajo de de la circunferencia primitiva ( ver figura 7 ).
Este fenómeno se debe a que aquí es donde mejor
puede desarrollarse la grieta sin "limarse", ya que la velocidad de
deslizamiento es muy pequeña.

figura 7: Picadura en los dientes de
engranajes.

b) Desgaste. Esta falla es propia de las transmisiones
no lubricadas, y se caracteriza por la disminución del
espesor del diente en la zona de la cabeza y del pié, que
es donde mayor velocidad de
deslizamiento existe ( ver figura 8 ).

figura ,8: Desgaste en los dientes de
engranajes.

c) Deformación plástica de la superficie
de los dientes o fluencia friccional. Esta falla se produce en
transmisiones altamente cargadas, y se caracteriza por la
fluencia del material hacia los extremos o centro del diente en
dependencia de si la rueda es conducida o conductora. ( ver
figura 9 )

figura ,9: Deformación
plástica de los dientes de las transmisiones por
engranajes

d) Fractura del diente. Esta falla se produce tanto en
transmisiones lubricadas como no lubricadas. La misma se puede
producir debido a la fatiga o a sobrecargas instantáneas.
La misma se produce en el pié del diente ( ver figura 10
).

figura 10: Fractura de los dientes de
las transmisiones por engranajes

5. Influencia de la
corrección en la disminución de las fallas de las
transmisiones por engranajes.

Cuando se presenta una falla en una transmisión
por engranajes el proyectista trata de resolverla inmediatamente
con la elevación de la calidad del
material; sin embargo muchas fallas se pueden retardar e
inclusive evitar con ligeras modificaciones a través del
uso de las correcciones.

Influencia de la corrección en la falla por
picadura de las transmisiones por engranaje.

La picadura o fatiga superficial, consiste en el
desprendimiento de párticulas de metal, de las superficies
de trabajo de los dientes, asociada a la acción sobre
éstas de tensiones de contacto de carácter
cíclico, en presencia del lubricante en la
transmisión.

Durante el funcionamiento de la transmisión, de
acuerdo de la magnitud de las tensiones de contacto, se
desarrollan en la superficie grietas de fatiga, que tienen su
origen en defectos de la superficie o del interior del metal. La
orientación de las mismas está intimamente
relacionada con las fuerzas de fricción sobre la
superficie, de suerte que las grietas, una vez desarrolladas,
mediante un proceso de fisuración progresiva quedan
orientadas en la dirección de las fuerzas de fricción
. Dado que la orientación de estas fuerzas sobre la rueda
conductora, es diferente y contraria a la de la conducida en la
zona de la cabeza y del pie del diente respectivamente, las
fisuras de fatiga se desarrollan en la dirección de estas fuerzas tal como se
muestra en la
figura 11.

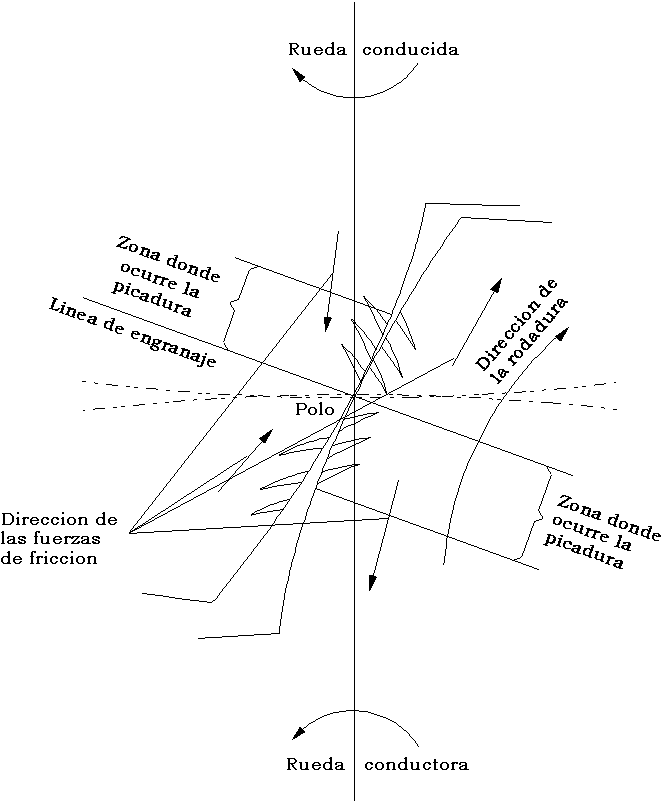
Figura 11: Desarrollo
de la grieta en los dientes.

El desarrollo
posterior de las grietas, una vez que alcanzan la superficie,
está intimamente relacionado con la presencia del
lubricante en la transmisión . En la figura 11 se muestra la
dirección del movimiento de
rodadura entre los dientes. El contacto comienza en el pie del
diente de la rueda conductora y la cabeza de la conducida y se va
extendiendo hacia la cabeza de la conductora y el pie de la
conducida. Esto determina que las grietas que se encuentran en el
pie de los dientes de ambas ruedas entran en la zona de contacto
por su abertura exterior, de manera que el aceite que se
encuentra en el interior de la grieta queda bloqueado y la
presiona abriéndola. Este proceso al repetirse
sucesivamente provoca el desprendimiento de las partículas
de metal. Al mismo tiempo, las
grietas que se encuentran en las superficies de la cabeza de los
dientes entran en contacto por le fondo y durante la rodadura el
aceite es desalojado del interior. En esta situación, las
grietas no experimentan la presión
del aceite y no se desarrollan los hoyos de picadura. La
picadura, pues, sólo se desarrolla en el pie de los
dientes, fundamentalmente en la zona próxima al polo donde
la carga específica es mayor.

Este proceso de picadura está directamente
relacionado con la presencia delas tensiones de contacto de
carácter cíclico que son, en definitiva las que dan
origen a las grietas de fatiga. Cualquier modificación de
la geometría
que disminuya la magnitud de las tensiones de contacto reduce la
posibilidad de aparición de estas grietas y disminuye la
tendencia de la superficie a la destrucción por
picadura.

En las transmisiones por engranaje las tensiones de
contacto se determinan según la ecuación de Hertz,
considerando las superficies de los dientes en las proximidades
de los puntos de contacto como dos cilindros, para este caso
particular:

Dado que el módulo de elasticidad E es
constante, las tensiones de contacto dependen de la carga
específica q y del radio de curvatura reducido
r . La expresión
del radio de curvatura reducido para una transmisión dada
es:

El término r P+r C = AB = constante (Figura. 12),
por lo que el radio de curvatura reducido es una función
inversa del producto r
P.r
C , y éste alcanza su valor máximo
cuando r
P = r
C, o sea en el punto medio de la línea
teórica de engranaje AB.

Figura 12. Línea práctica de
engranajes

En la figura 13 se muestra la curva de variación
del radio de curvatura reducido a lo largo de la línea
teórica de engranaje. En el caso de los engranajes
cilíndricos de dientes rectos la carga específica
varía a lo largo de la línea práctica de
engranaje. Si simplificamos el esquema de variación de la
carga específica y consideramos que esta varía de
q/2 a q, podemos obtener las curvas de variación de las
tensiones de contacto. De este análisis se desprende que para obtener el
valor mínimo de las tensiones de contacto, es necesario
lograr un desplazamiento de la línea práctica de
engranaje, mediante una corrección tal que ubique la misma
simétricamente respecto al punto C. En la figura 14 se
muestran las modificaciones del radio de curvatura y de las
tensiones de contacto al desplazarse la línea de engranaje
mediante la corrección. Para lograr esta condición
debe cumplirse que corresponde al valor de la corrección
de altura necesario para obtener el mínimo valor de las
tensiones de contacto, o lo que es lo mismo, la máxima
resistencia a la
picadura. Es obvio que el valor del coeficiente de
corrección obtenido debe ajustarse teniendo en cuenta las
limitaciones establecidas anteriormente.

Una forma evidente de disminuir las tensiones de
contacto para el caso de la corrección angular es aumentar
en todo lo posible los radios de curvatura, y logar una
combinación óptima de los valores
del coeficiente de corrección para el piñon y para
la corona. En las tablas 5 y 6 se muestran los valores del
coeficiente de corrección para máxima resistencia a la
picadura para corrección de altura y para
corrección angular.

Figura 13. Tensiones superficiales en ruedas no
corregidas

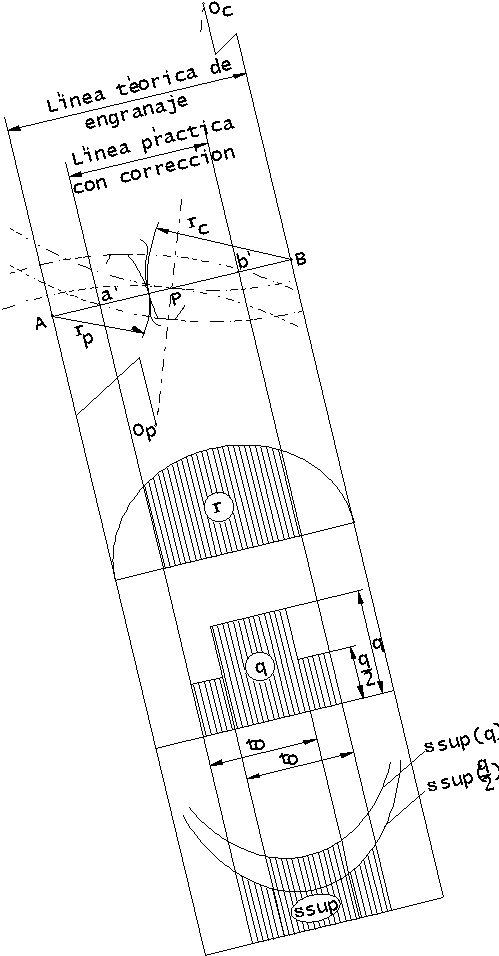
Figura14. Tensiones superficiales en ruedas
corregidas

Influencia de la corrección en la falla por
desgaste de las transmisiones por engranaje.

El desgaste de las ruedas dentadas es una función
de la potencia
eslecífica de las fuerzas de fricción. El valor del
trabajo específico de las fuerzas de fricción se
puede calcular por la expresión:

Donde

A – Trabajo específico de las fuerzas de
fricción.

f – Coeficiente de fricción.

Pn – Fuerza normal
entre los dientes.

Vdes- Velocidad de deslizamiento entre los
dientes.

S – Area de contacto en la unidad de tiempo.

El cociente Vdes / S se conoce como deslizamiento
específico, de aquí que el desgaste será
tanto mayor cuanto mayor sea el mismo.

Debido a que el máximo deslizamiento
específico tiene lugar en los punto inicial y final de la
línea de engranajes, entonces el máximo desgaste se
produce en el pie y en la cabeza de los dientes. En el polo de
los engranajes no hay deslizamiento de los perfiles, por lo que
el desgaste en la zona circunpolar es mínimo ( ver figura
15 ).

El deslizamiento específico es mayor al inicio
del contacto que al final de este; en consecuencia el desgaste es
mayor en el pié que en la cabeza. Mediante las
corrrecciones ya sean de altura o angulares se puede lograr un
desplazamiento total de la línea práctica de
engranajes ab que permita igualar la magnitud de los
deslizamientos específicos al comienzo y al final de esta
línea. En este caso se logra el desgaste mínimo de
la transmisión.

La velocidad de deslizamiento de un punto K ( ver figura
15 ) se puede calcular por la expresión :

Esta velocidad de deslizamiento juega un papel decisivo
en la potencia
consumida en vencer la fricción, y las condiciones de
máxima resistencia al desgaste se garantizarán
ubicando la línea de engranajes en una zona donde su valor
sea el menor posible y esté compensado tanto a la entrada
como a la salida del contacto.

Obsérvese por ejemplo que al dar una
corrección de altura ( positiva al piñón y
nagativa a la corona ), el diámetro exterior del
piñón se hace mayor, y el de la corona disminuye,
cambiando la ubicación de los puntos a y b , es decir se
puede mover la línea práctica de engranajes y
ubicarla en kla zona que se desee. Teniendo en cuenta estos
criterios se elaboró un programa de
computación y se determinaron los valores
óptimos de corrección de altura para máxima
resistencia al desgaste. Estos valores aparecen en la tabla
4.

De manera similar se procedió con los valores del
coeficiente de corrección para las diferentes fallas en el
caso particular de la corrección angular. Los mismos
aparecen en la tabla 6.

figura 15: deslizamiento en las transmisiones por
engranajes

6. Formas en que se
pueden presentar los problemas de
engranajes corregidos.

La corrección del dentado de una
transmisión por engranajes no siempre es una obligacion
para el diseñador, no obstante el empleo de las
mismas es muy conveniente de acuerdo a lo planteado en los
epigrafes anteriore. A continuación se exponen las formas
más comunes de abordar los problemas
relacionados con la corrección de las transmisiones por
engranajes.

Primer caso:

La distancia entre centros es libre, es decir no viene
fijada de antemano. En este caso el proyectista puede elegir tres
soluciones:

a) No dar corrección, es decir usar engranajes
normales .

b) Dar una corrección angular teniendo en cuenta
las condiciones de trabajo de la transmisión.

c) Dar una corrección de altura teniendo en
cuenta el regimen de trabajo de la transmisión.

Segundo caso:

La distancia entre centros viene fijada de antemano. En
este caso se pueden presentar las siguientes soluciones.

a) Garantizar la distancia entre centros dada con una
pareja de ruedas normales cuyos números de dientes y
módulo den como resultado dicha distancia entre
centros.

b) De lograrse la situación anterior dar una
correccioñ de altura a dichas ruedas con vistas a atenuar
la falla que pudiera presentarse.

c) Elegir números de dientes para el
piñón y la corona, y un módulo dado de tal
manera que la distancia entre centros sea cercana a la fijada de
antemano, y llevarla a la misma mediante una corrección
angular, garantizando de paso una mayor resistencia a las fallas
que pudieran presentarse.

Ejemplos de cálculo.

Problema # 1 – Se desea diseñar una
transmisión por engranajes con m = 5, Zp =15, y Zc = 63.
Determine las posibles soluciones.

Solución:

Se puede:

Dar una corrección de altura y eliminar el
socavado. Posteriormente aplicar las fórmulas de la tabla
2 para hallar los parámetros
geométricos.

Dar una corrección de altura para máxima
resistencia a la picadura ( según tabla 5 ).
Posteriormente aplicar las fórmulas de la tabla 2 para
calcular todos los parámetros geométricos de la
transmisión.

Dar una corrección angular de acuerdo a la falla
posible ( según tabla 6 ), y calcular los
parámetros geométricos de las ruedas según
la tabla 3

Problema # 2- Determinar los parámetros
geométricos de una transmisión por engranajes
cilíndrica de dientes rectos con los siguientes datos:

módulo (m) = 5

número de dientes del piñón (Zp) =
16

número de dientes de la corona (Zc) =
48

Existe la restricción de que la distancia entre
centros (aw) tiene que ser exactamente de 160 mm. Se desea
además atenuar en lo posible la falla de la
picadura.

Solución:

Primeramente se debe calcular la distancia entre centros
que normalmente tiene la transmisión sin ser
corregida:

Como la distancia calculada coincide con la dada como
dato, en este caso no se debe dar una corrección angular,
ya que entonces la distancia variaría. Por tanto para
atenuar la falla de picadura la única solución
posible es dar una corrección de altura para máxima
resistencia a la picadura. Los coeficientes de corrección
se pueden elegir de la tabla 5. Para los números de
dientes dados, X1 = – X2 = 0,64.

Con esos valores del coeficiente de corrección, y
aplicando las fórmulas de la tabla 2 se determinan todos
los parámetros geométricos de la
transmisión.

Problema # 3- Determinar los parámetros
geométricos de una transmisión por engranajes
cilíndrica de dientes rectos con los siguientes datos:

módulo (m) = 8

número de dientes del piñón (Zp) =
18

número de dientes de la corona (Zc) =
65

Existe la restricción de que la distancia entre
centros (aw) tiene que ser exactamente de 340 mm. Se desea
además atenuar en lo posible la falla de
desgaste.

Solución:

Primeramente se debe calcular la distancia entre centros
que normalmente tiene la transmisión sin ser
corregida:

Como la distancia calculada no coincide con la dada como
dato, en este caso se debe dar una corrección angular para
llevar la distancia entre centros (a) de 332 mm a (aw) 340
mm.

El primer paso es hallar el ángulo de montaje que
hay que lograr en la transmisión:

A continuación se procede a calcular el
coeficiente sumario de corrección:

El siguiente paso es distribuir el coeficiente sumario
de corrección entre el piñón y la corona,
teniendo en cuenta que se pide máxima resistencia al
desgaste.

Los valores recomendados de la tabla 3.6 para este tipo
de falla son los siguientes:

X1 = 0,71 y X2 = 1,35 . La suma de ellos da un valor de
2,06, superior al valor necesario para el ajuste de la distancia
entre centros. Una decisión a tomar puede ser darle al
piñón el valor X1 = 0,71, y el resto para llegar a
1,084 darselo a la corona. Posteriormente aplicando las
expresiones de la tabla 3 calcular todos los parámetros
geométricos de ambas ruedas.

Problema # 4 – Determinar los parámetros
geométricos de una transmisión por engranajes
cilíndrica de dientes rectos con los siguientes
datos:

módulo (m) = 8

número de dientes del piñón (Zp) =
18

número de dientes de la corona (Zc) =
65

No existen restricciones en la distancia entre centros
(aw). Se desea además atenuar en lo posible la falla de
desgaste.

Solución:

En este caso como no existen restricciones en la
distancia entre centros, se procede directamente a seleccionar
los coeficientes de corrección óptimos para
máxima resistencia al desgaste de la tabla 6: X1 = 0,71 y
X2 = 1,35 . La suma de ellos da un valor de 2,06, siendo entonces
este el valor del coeficiente sumario de
corrección.

El siguiente paso es hallar el ángulo de montaje
que hay que lograr en la transmisión:

A continuación se procede a calcular el
coeficiente de compensación D y:

La distancia entre centros se determina por la
expresión:

Posteriormente aplicando las expresiones de la tabla 3
se calculan todos los parámetros geométricos de
ambas ruedas.

Tabla # 4 Correccion de altura para
máxima resistencia al desgaste

ZcZp	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29
20	18	18	18	18	16	12	6	4
21	24	24	24	24	19	15	11	7	4
22	30	30	30	27	22	19	14	11	7	4
23	35	35	34	29	25	21	17	14	10	7	4
24	41	41	36	32	28	24	20	16	13	10	6	3
25	47	43	39	34	30	26	23	19	16	12	9	6	3
26		45	41	37	35	29	25	22	18	15	12	8	6	4
27		47	43	39	35	31	27	24	21	17	14	11	8	6	3
28		49	45	41	37	33	30	26	23	20	17	14	11	8	5	3
29		50	46	43	39	35	32	28	25	22	19	16	13	10	8	5	3
30		52	48	44	41	37	34	30	27	24	21	18	15	13	10	7	5	3
31			50	46	42	39	35	32	29	26	23	20	17	15	12	10	7	5
32			51	47	44	41	37	34	31	28	25	22	19	17	14	12	9	7
33			52	49	46	42	39	36	33	30	27	24	21	19	16	14	11	9
34			54	50	47	44	40	37	34	31	28	26	23	20	18	15	13	11
35			55	52	48	45	42	39	36	33	30	27	25	22	20	17	15	13
36			56	53	50	46	43	40	37	35	32	29	26	24	21	19	17	14
37				54	51	48	45	42	39	36	33	31	28	25	23	21	18	16
38				55	52	49	46	43	40	37	35	32	30	27	25	22	20	18
39				56	53	50	47	44	42	39	36	34	31	29	26	24	22	19
40				57	54	51	48	46	43	40	38	35	32	30	28	25	23	21
41				58	55	52	50	47	44	41	39	36	34	31	29	27	24	22
42				59	56	53	51	48	45	43	40	38	35	33	30	28	26	24
43				60	57	54	52	49	46	44	41	39	36	34	32	29	27	25
44					58	55	53	50	47	45	42	40	38	35	33	31	29	26
45					59	56	54	51	48	46	44	41	39	36	34	32	30	28
46					60	57	55	52	49	47	45	42	40	38	35	33	31	29
47					61	58	55	53	50	48	46	43	41	39	36	34	32	30
48					61	59	56	54	51	49	47	44	42	40	38	35	33	31
49					62	60	57	55	52	50	48	45	43	41	39	37	34	32
50					63	60	58	55	53	51	48	46	44	42	40	38	36	34
51					64	61	59	56	54	52	49	47	45	43	41	39	37	35
52					64	62	59	57	55	52	50	48	46	44	42	40	38	36
53						62	60	58	55	53	51	49	47	45	43	40	39	37
54						63	61	58	56	54	52	50	48	45	43	41	39	38
55						64	61	59	57	55	53	50	48	46	44	42	40	38
56						64	62	60	58	55	53	51	49	47	45	43	41	39

Nota: Los valores tomados de la tabla deben ser
multiplicados por 0,01. Cuando se desee determinar el coeficiente
de corrección para un número de dientes, y no
aparezca su valor en la columna correspondiente, debe tomarse el
último valor que aparece en dicha columna. Por ejemplo
para Zp = 12 y Zc = 40 el valor del coeficiente de
corrección X1 = -X2 será 0,47

Tabla # 5 Corrección de altura
para máxima resistencia a la picadura

ZcZp	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29
20	17	17	17	17	17	15	10	5
21	23	23	23	23	23	20	15	10	5
22	30	30	30	30	30	25	20	15	10	5
23	35	35	35	35	35	30	25	20	14	10	5
24	41	41	41	41	40	34	29	24	19	14	10	5
25	47	47	47	47	47	39	34	29	24	19	14	10	5
26		52	53	53	49	43	38	33	28	23	18	14	9	5
27			56	58	53	48	43	38	33	28	23	18	14	9	5
28				60	57	52	47	42	37	32	27	23	18	14	9	5
29					62	56	51	46	41	37	32	27	22	18	13	9	4
30					64	61	56	51	46	41	36	31	27	22	18	13	9	4
31						65	60	55	50	45	40	36	31	26	22	17	13	9
32						68	64	59	54	19	45	40	35	31	27	22	17	13
33							68	63	58	53	49	44	39	35	30	26	21	17
34							71	67	62	57	53	48	44	39	35	30	26	21
35								71	66	62	57	52	48	43	39	34	30	25
36								75	70	66	61	56	52	47	43	38	34	30
37									74	70	65	60	56	51	47	42	38	34
38									79	74	69	64	60	55	51	46	42	38
39										78	73	68	64	59	55	50	46	42
40										82	77	72	68	63	59	54	50	46
41											81	76	72	67	63	58	54	49
42											85	80	75	71	67	62	58	53
43												84	79	75	70	66	62	57
44												88	83	79	74	70	65	61
45												89	87	82	78	74	69	65
46													91	86	82	77	73	69
47													92	90	86	81	77	73
48														94	89	85	81	76
49														95	93	89	84	80
50															97	92	88	84
51															98	96	92	88
52																100	95	91
53																101	99	95
54																	103	99
55																	104	102
56																		105

Nota: Los valores tomados de la tabla deben ser
multiplicados por 0,01. Cuando se desee determinar el coeficiente
de corrección para un número de dientes, y no
aparezca su valor en la columna correspondiente, debe tomarse el
último valor que aparece en dicha columna. Por ejemplo
para Zp = 14 y Zc = 40 el valor del coeficiente de
corrección X1 = -X2 será 0,56

Tabla # 3,6 Corrección angular
para atenuar las diferentes fallas de los engranajes.

Zc Zp	12		15		18		22		28		34
	X1	X2	X1	X2	X1	X2	X1	X2	X1	X2	X1	X2
	0,30	0,61	0,34	0,64	0,54	0,54
18	0,57	0,25	0,64	0,29	0,72	0,34
	0,49	0,35	0,48	0,46	0,54	0,54
	0,30	0,66	0,38	0,75	0,60	0,64	0,68	0,68
22	0,62	0,28	0,73	0,32	0,81	0,38	0,95	0,39
	0,53	0,38	0,55	0,54	0,60	0,63	0,67	0,67
	0,30	0,88	0,26	1,04	0,40	1,02	0,59	0,94	0,86	0,86
28	0,70	0,26	0,79	0,35	0,89	0,38	1,04	0,40	1,26	0,42
	0,57	0,48	0,60	0,63	0,63	0,72	0,71	0,81	0,85	0,85
	0,30	1,03	0,13	1,42	0,30	1,30	0,48	1,20	0,80	1,08	1,01	1,01
34	0,76	0,22	0,83	0,34	0,93	0,37	1,08	0,38	1,30	0,36	1,38	0,34
	0,60	0,53	0,63	0,72	0,67	0,82	0,74	0,90	0,86	1,0	1,0	1,0
	0,30	1,30	0,20	1,53	0,29	1,48	0,40	1,48	0,72	2,33	0,9	1,30
42	0,75	0,21	0,92	0,32	1,02	0,36	1,18	0,38	1,24	0,31	1,31	0,27
	0,63	0,67	0,68	0,88	0,68	0,94	0,76	1,03	0,88	1,12	1,0	1,16
	0,30	1,43	0,25	1,65	0,32	1,63	0,43	1,60	0,64	1,60	0,80	1,58
50	0,58	-0,16	0,97	0,31	1,05	0,36	1,22	0,42	1,22	0,25	1,25	0,20
	0,63	0,77	0,66	1,02	0,70	1,11	0,76	1,17	0,91	1,26	1,0	1,31
	0,30	1,69	0,26	1,87	0,41	1,89	0,53	1,80	0,70	1,84	0,83	1,79
65	0,55	-0,35	0,80	0,04	1,10	0,40	1,17	0,36	1,19	0,20	1,23	0,15
	0,64	1,0	0,67	1,22	0,71	1,35	0,76	1,44	0,88	1,56	0,99	1,55
	0,30	1,26	0,30	2,14	0,48	2,08	0,61	1,99	0,75	2,04	0,89	1,97
80	0,54	-0,54	0,73	-0,15	1,14	0,40	1,15	0,26	1,16	0,12	1,19	0,07
	0,65	1,18	0,67	1,36	0,71	1,61	0,76	1,73	0,87	1,85	0,98	1,81
	0,30	2,90	0,36	2,32	0,52	2,31	0,65	2,19	0,80	2,26	0,94	2,22

En esta tabla para cada número de dientes, el
primero de los renglones corresponde a los valores de
corrección para máxima resistencia a la picadura,
el segundo para máxima resistencia a la fractura , y el
tercero para máxima resistencia al desgaste

7.
Bibliografía

A.G.M.A. "Honing the competitive edge. Machine Design" #
19 vol.65. Set. 24 1993.

A.G.M.A. Standarad 2101C95., Fundamental Rating and
Calculation Methods for Involute Spur and Helical Gears Teeth.,
American Gear Manufacturers Association, Alexandría, VA,
1995.

Abramov. B.M. "Kolibanie priemozubix zubchatij
koliés". Editorial Jarkobskovo Universitieta Jarkov
1968.

AGMA Publications Catalog., Global Engineering
Documents., Englewood, 1998-1999.

Airapetov E. L. "Cargas dinámicas en el contacto
simultáneo de varios pares de dientes". Revista
Viestnik Mashinostroienia. #8, 1991. Moscú.

Airapetov E.L. "Influencia de las deformaciones
elásticas de los dientes en los parámetros de
contacto de los dientes en transmisiones cilíndricas de
dientes rectos". Revista
Viestnik Mashinostroienia. 8 .1990.

Baránov, G.G. Curso de la teoría de
mecanismos y máquinas.
/ G. G, Baránov. – 2da ed –
Moscú : Editorial MIR, 1985. – 524p.

Black Paul H. "Machine Design" Editorial Mc Graw Hill,
New York
1955.

Borisenkov V.A."Perfeccionamiento del cálculo al
contacto de las transmisiones evolventes cilíndricos"
Revista Viestnik Mashinostroienia # 8 1985.

Bragin V.V. "Determinación de las cargas
específicas y tensiones en los dientes de una
transmisión dentada cilíndrica de dientes rectos".
Revista Viestnik Mashinostroienia No.7 1984.

Bragin V.V. "Resistencia a la flexión y rigidez
del diente de ruedas cilíndricas de dientes rectos".
Revista Viestnik Mashinostroienia # 11 1987 .

Broersma I. "Design of Gears.". Editorial Industrial
Press Inc. New York 1975.

Buckingham E. "Manual of Gear
Design. Section two .Spur and internal Gears". Editorial
Industrial Press Inc. New York 1971.

Cherkashin B.P. Optimización Multicriterial de
las transmisiones por engranajes. V.M. No.1, 1988.

Cherkashin, B. P., Selección
de los coeficientes de corrección óptimos para los
dientes de un engranaje, Viestnik Mashinostroienia, No.8, pp. 84
– 95, 1980

Chernavskij S.A. Diseño
de transmisiones Mecánicas. MIR. Moscú.
1984.

Colectivo de Autores. Técnica de Engranajes. Veb
Verlag Technik. Berlín. 1978.

Dobrovolskij V. Elementos de Máquinas. MIR.
Moscu. 1970.

Dorofieiev V.L."Determinación exacta de las
cargas dinámicas en las transmisiones dentadas". Revista
Viestnik Mashinostroienia #8 1986 .

Dorofieiev. V.L. "Bases de cálculo de fuerzas y
tensiones durante el contacto de las transmisiones
cilíndricas dentadas". Revista Viestnik Mashinostroienia #
3 1983 .

Drosdov Y. Diferentes Métodos de Cálculo
de desgaste en ruedas dentadas. V.M. No. 11, 1991.

Drozdov Yu. "Diferentes métodos de cálculo
de desgaste en ruedas dentadas".Revista Viestnik
Mashinostroienia. 11 .1991.

Dudley, D. W., Manual de
Engranajes Diseño,
Manufactura y
Aplicación de Engranajes. Continental, S.A., México,
1980.

"Efficiency of gear drives". Rev. Trans. of the ASME,
vol 40, pag 107 – 1918.

Fuentes Losa J. Selección del desplazamiento en
engranajes cilíndricos basada en el recubrimiento y el
equilibrio
óptimo de deslizamientos específicos. I Congreso
Ibero-Americano de Ingenieria Mecánica. España.
1993.

Fuentes, A., Pedrero, J.I., Análisis de la Tensión de
Flexión en Engranajes Cilíndricos de Perfil de
Evolvente, Anales de Ingeniería Mecánica, Vol. 2, pp. 146-151,
1996.

Fuentes, Aznar A., Modelo de
Cálculo a Flexión de Engranajes Cilíndricos
de Perfil de Evolvente. Tesis
Doctoral, U.N.E.D., Madrid, 1996.

García Masiá, C., Optimización del
Diseño de Engranajes por Análisis
Paramétrico, Tesis
Doctoral, UNED, Madrid, 1994.

Gay Charles E. How to design to minimize wear in gears.
M.D. 1970.

Goluvev Y. Teoria de los Mecanismos y Máquinas.
Ciencia y
Tecnica.
1967.

González Rey, G., Apuntes para el Cálculo
de Engranajes Cilíndricos según la norma I.S.O. del
Comité Técnico 60. E.P.U. de Zamora, I.S.P.J.A.E.,
Ciudad Habana., 1998.

González Rey, G., y García, M.E.,
Coeficientes de cargas dinámicas en Engranajes
Cilíndricos según ISO 6336,
3er Congreso Iberoamericano de Ingeniería Mecánica, ISPJAE, Ciudad
Habana, 1997.

González Rey, G., y García, M.E., Trabajos
en la normalización internacional del
cálculo de los engranajes cilíndricos y
cónicos, Ingeniería Mecánica, pp 37-42,
ISPJAE, 1997.

GOST 21354-87, Cálculo de Transmisiones por
Engranajes Cilíndricas de dientes rectos de perfil de
evolvente, Gosudartsviennij Standart, Moscú,
1989.

Goytisolo R. Moya J. "Analisis de la lubricación
en el reductor PM 400. Rev. Centro Serie Construcción de maquinaria. Año I #2
. Julio-Dic. 1976.

Goytisolo R., Moya Rodriguez J.L. Corrección de
altura para máxima resitencia a la picadura. CENTRO. UCLV.
1977.

Goytisolo R., Moya Rodriguez J.L. Influencia de la
corrección en la lubricación de las transmisiones
por engranajes. CENTRO. UCLV. 1976.

Goytisolo, R., Moya, J.L., Cálculo de la
corrección de altura en los engranajes, Tecnología
Mecánica, No. 1, pp. 44–48, 1991.

Hennigs G. "Determinación del estudio de
deterioro del flanco de los dientes y su superficie a
través del método de la mancha de contacto".
Revista Cientifica de la Universidad
Técnica de Magdeburgo. Vol 23 # 3 1980.

Henriot G. "Manual práctico de engranajes".
Editorial Marcombo S.A. Barcelona
1977.

Henriot, G., Traité Théorique et Pratique
des Engrenages. Villars, París. 1991.

Kopf L. A. "Determinación de las cargas en el
desgaste progresivo en las transmisiones dentadas". Revista
Viestnik Mashinostroienia. #1, 1985. Moscú.

Kudriatzev. V.N."Acerca del problema de la
valoración exacta de la capacidad portadora de las
transmisiones dentadas cilíndricas".Revista Viestnik
Mashinodtroienia # 3 1983 .

Lafont, P., Cálculo de Engranajes Paralelos,
ETSII, Madrid, 1993.

Lewis, W., Investigation of Strenght of Gear Teeth,
Proc. of Engineers Club, Philadelphia, P.A, pp. 16-23,
1892.

Linke. H. "Capacidad de carga de transmisiones dentadas
y engranajes. Evento sobre transmisiones dentadas". Dresden
1983.

Litvin F.L. "Teoría de los engranajes" Editorial
Nauka Moscú – 1968.

Litvin, F.L., Applied Theory of Gearing: State of the
Art, Journal of Mechanical Design, Vol. 117, pp 78-82, junio,
1995.

Machado Rodríguez, A., Moya Rodríguez, J.,
Optimización de los Engranajes Cilíndricos de
dientes rectos de los molinos de caña de azúcar,
Centro Azúcar, N0 2, 1998.

Moring Faires V. Design of Mashine Elements. Mcmillan
Co. 1955.

Moya R.J. Goytisolo E.R. "Analisis cinemático y
dinámico de transmisiones por engranajes que trabajan con
variación de la distancia entre centros." Actas del Primer
Congreso Iberoamericano de Ingeniería Mecánica.
Madrid Setiembre de 1993.

Moya Rodriguez J.L. Teoría de Mecanismos y
Máquinas. Proyecto de
Curso. UCLV. 1988

Nieman G. Elementos de Máquinas (Tratado
Teórico Práctico). Editorial Labor S.A. Madrid.
1967.

Reshetov, D. Elementos de máquinas. / D. Reshetov
– La Habana: Editorial Pueblo y Educación, 1985
– 829p.

Shekin B.M. Modelación y Optimización de
las transmisiones por engranajes. V.M. No. 1, 1987.

Shigley, J.E., Diseño en Ingeniería
Mecánica, McGraw-Hill, 1990.

Spott M.F. Proyecto de
Elementos de Máquinas. Editorial Reverte S.A. Argentina.
1982.

Spotts M F "Design of machine elements ".Editorial
Prentice Hall Inc. Englewood Cliffs. New Jersey 1990

Wilcox, L., Coleman, W., Application of Finite Elements
to the Analysis of Gear Tooth Stresses, ASME Journal of
Engineering for Industry, Vol. 95, pp 1139-1148, 1973.

Zirpke K. "Zahnrader".Veb Fachbuch Verlag Leipzig
1980.

Trabajo enviado y realizado por:
Dr.Jorge Laureano Moya Rodríguez
Dr. Rafael Goytisolo Espinosa

Departamento de Mecánica Aplicada y Dibujo
Facultad de Ingeniería Mecánica
Universidad
Central de Las Villas
Teléfono: 53 – 422 – 281630
FAX: 53
– 422 – 281608
Noviembre del 2000.